Is Zero Even Or Odd? Understanding The Nature Of Zero In Mathematics

06 May, 2025

Is zero even or odd? This question has intrigued mathematicians, students, and curious minds alike for centuries. The number zero holds a unique position in the number line and has properties that can sometimes be counterintuitive. In this article, we will delve into the nature of zero, explore its mathematical properties, and clarify why zero is classified as an even number.

Understanding whether zero is even or odd is more than just a trivial pursuit; it has implications in various fields of mathematics, including algebra, number theory, and even computer science. By the end of this article, you will have a comprehensive understanding of zero’s classification and its significance in mathematics.

Join us as we embark on this mathematical journey, unraveling the mysteries of zero and solidifying its status as an even number. We will also provide insights into the historical context of zero, its properties, and its applications in various mathematical concepts.

1. Understanding Zero: Definition and History
2. What Does It Mean to Be Even or Odd?
3. Properties of Zero

3.1 Zero in Arithmetic Operations
3.2 Zero in Geometry

4. Why Zero is Considered Even
5. Applications of Zero in Mathematics
6. Conclusion
7. References

1. Understanding Zero: Definition and History

Zero is a numerical digit that represents the absence of a quantity. It is a fundamental concept in mathematics, serving as a placeholder in positional numeral systems and as a number in its own right. The history of zero dates back to ancient civilizations, including the Babylonians and the Mayans, who recognized the need for a symbol to denote nothingness or the absence of value.

In the context of the number line, zero acts as the dividing point between positive and negative numbers. Its introduction into mathematics has revolutionized calculations, paving the way for advancements in algebra and calculus. Understanding zero's historical context gives us a better appreciation for its significance in the mathematical world.

2. What Does It Mean to Be Even or Odd?

To classify a number as even or odd, we first need to understand the definitions:

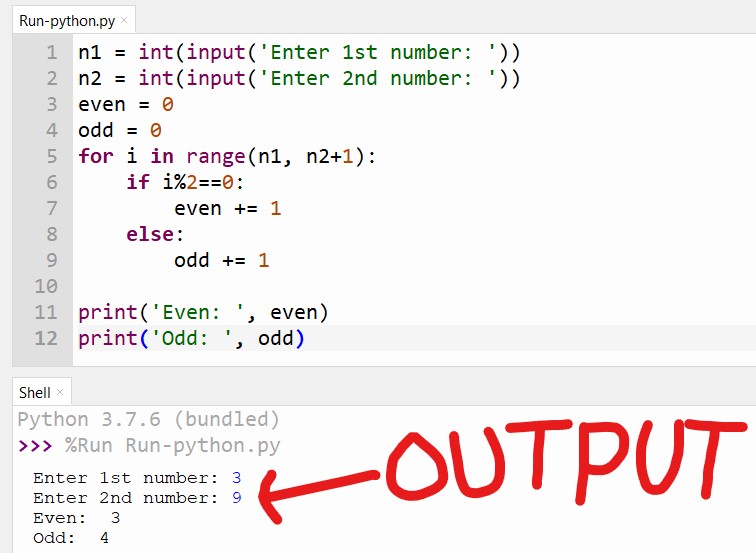
An **even number** is any integer that can be divided by 2 without leaving a remainder. In mathematical terms, an even number can be expressed as 2n, where n is an integer.
An **odd number** is an integer that cannot be divided by 2 evenly, meaning it leaves a remainder of 1. Odd numbers can be represented as 2n + 1.

Now that we have a clear understanding of what it means to be even or odd, we can analyze where zero fits into this classification.

3. Properties of Zero

Zero possesses unique properties that distinguish it from other numbers. Understanding these properties is crucial for grasping why zero is classified as an even number.

3.1 Zero in Arithmetic Operations

Zero has several important properties in arithmetic:

**Addition**: Adding zero to any number does not change its value (e.g., x + 0 = x).
**Subtraction**: Subtracting zero from any number also leaves the number unchanged (e.g., x - 0 = x).
**Multiplication**: Any number multiplied by zero results in zero (e.g., x * 0 = 0).
**Division**: Dividing zero by any non-zero number yields zero (e.g., 0 / x = 0), but division by zero is undefined.

3.2 Zero in Geometry

In geometry, zero plays a vital role as well. A point on a Cartesian plane is often represented by coordinates (0, 0), indicating its position at the origin. In this context, zero serves as a reference point for measuring distances and angles.

4. Why Zero is Considered Even

Now, let’s address the main question: Is zero even or odd? To determine this, we can apply the definition of even numbers:

Since zero can be expressed as 2n (where n = 0), it fits the criteria for being an even number. Therefore, we can conclude that zero is indeed an even number.
Additionally, dividing zero by 2 yields zero, confirming that zero is even (0 ÷ 2 = 0).

This classification aligns with mathematical conventions and is widely accepted in the mathematical community. Understanding why zero is even helps to eliminate confusion and allows for a clearer comprehension of mathematical principles.

5. Applications of Zero in Mathematics

Zero is not only essential for theoretical mathematics but also has practical applications in various fields. Some of these applications include:

**Computer Science**: In binary code, zero plays a critical role as one of the two fundamental digits.
**Statistics**: Zero is used to denote the absence of a quantity in data analysis.
**Physics**: Zero is used in equations to represent a state of equilibrium or balance.
**Finance**: Zero can represent break-even points in profit and loss calculations.

6. Conclusion

In conclusion, zero is classified as an even number based on its mathematical properties and definitions. Understanding the nature of zero not only clarifies its classification but also highlights its significance in various mathematical applications. We encourage readers to engage with this topic further by leaving comments, sharing their thoughts, or exploring related articles on mathematics and its fascinating concepts.

7. References

Rosen, Kenneth H. "Discrete Mathematics and Its Applications." McGraw-Hill, 2012.
Weisstein, Eric W. "Zero." MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/Zero.html
Wells, David. "The Penguin Dictionary of Curious and Interesting Numbers." Penguin Books, 1997.

Details

Zero is even or odd 2 is even or odd Even and Odd numbers

Details

Free Printable Odd And Even Numbers Charts

Details

Detail Author:

Name : Delia Durgan
Username : antonette.simonis
Email : norwood.johnson@luettgen.com
Birthdate : 1988-07-08
Address : 96866 Mraz Stream Suite 861 Lake Kaelamouth, DE 73315
Phone : +1-956-521-0685
Company : Rolfson and Sons
Job : Transportation Attendant
Bio : Natus eos non non quis reprehenderit. Beatae rerum voluptatum et possimus enim. Minus in sint cum sunt rerum at autem quisquam. Ex a omnis omnis. Dolorum nemo deleniti consectetur enim deleniti.

Socials

twitter:

url : https://twitter.com/altenwerthh
username : altenwerthh
bio : Nesciunt ut ut quam amet omnis. Officiis consequuntur et ipsa dolorem numquam.
followers : 4548
following : 751

instagram:

url : https://instagram.com/hulda.altenwerth
username : hulda.altenwerth
bio : Quia veniam et sed nam ut. Qui totam nemo et ut nihil. Doloribus quo ea velit ut.
followers : 6880
following : 1331